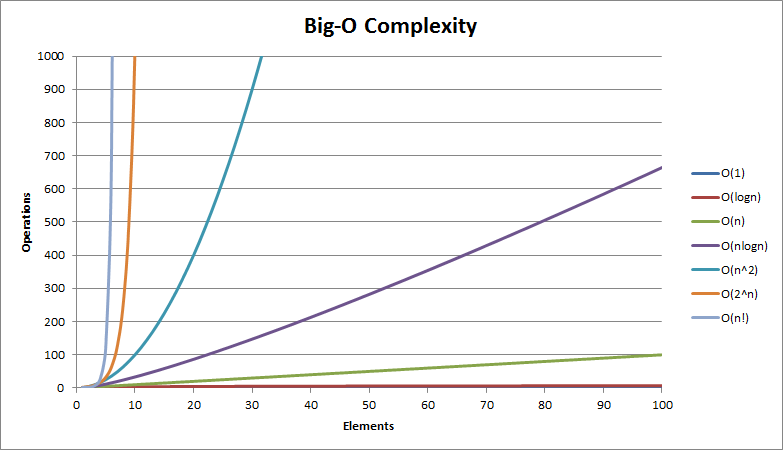
big O

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        sum += n.charCodeAt(i);
    }
    return sum;
}

• This is $O(N)$ because the runtime scales with the input (which is of size n)
• $O(2N)=O(N)$ because we drop constants because we only care about how it grows with the input. As you take it to infinity, the constants become irrelevant
• there are cases where $O(N^2)$ is faster than N, if N is sufficiently small
• big O notation is for considering the worst case scenario (upper bound)

1. growth is with respect to input
2. constants dropped
3. usually measure worst case

function sum_char_codes(n: string): number {
    let sum = 0;
    for (let i = 0; i < n.length; ++i) {
        for (let j = 0; j < n.length; ++j) {
            sum += charCode;
        }
    }

    return sum;
}

This is $O(N^2)$

• quicksort is an example of $n\log n$
  • you go over n characters, then half it then search n characters again and half it...
• binary search trees are $O(\log n)$

$O(\sqrt{n})$

• arrays are just contiguous memory spaces
• lists != arrays
• getting a value from an array is $O(N)$ (assuming you know the offset * width)
  • i.e. constant time
• arrays are fixed sizes; to grow it you need to reallocate it because when you initialize it you know its size

The two crystal ball problem

• given 2 balls that will break if dropped from high enough, determine where it will break
• you could start at 0 and linearly walk up to the point where it breaks
  • but you have 2 balls so you can do better than O(n)
• try jumping sqrt(n) each time with the first ball until it breaks
  • O(sqrt(n))

Bubble sort

• move largest number to end
  • move second largest to second last
    • ...continue
• gauss: sum of numbers in range (1..=n) is n(n+1)/2
• $$\sum _{n=1}^{n}n=\frac{n(n+1)}{2}$$
• O(n^2)